[AtCoder] ABC 113 D – Number of Amidakuji

2019年5月11日2019年5月15日

問題

方針

ある高さの正しい横棒の配置

ある高さの横棒の配置のパターンを考えます。横棒は縦棒の間に置くことができるので、縦棒の本数 \( W \) が \( W = 1 \) のときは横棒を置くことができません。そうではないとき、縦棒の間に横棒を置くか置かないかの \( 2 \) 通りがあるので、全体で \( 2^{W – 1} \) 通りあります。このパターンは \( W – 1 \) ビットのビット列として表すことができます。

次にこのパターンから正しくない横棒の置き方をしているものを取り除きます。これは得られたビット列において、\( 1 \) が隣り合うときとなります。例えば、\( W = 4 \) のとき、以下のパターンが得られます。

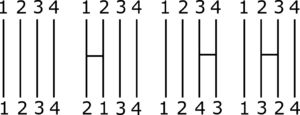
これをビット列で表現すると、左から、

\( 000 \), \( 100 \), \( 001\), \( 010 \)

となります。

動的計画法

横棒の置き方は高さに依存せずにおくことができるので、高さ \( 1 \) から \( H \) まで順々に数え上げていくことができます。ここで、配列 \( dp[i][j] \) 高さ \( 0 \) における縦棒 \( 1 \) から高さ \( i \) における縦棒 \( j \) までの行き方とします。初期値は、\( dp[0][0] = 1\) とします。また、以降では縦棒の添え字を \( 0 \) オリジンとして考えます。この配列の更新の仕方は、上記の画像を例にすると次のように記述でます。

\[
\begin {align}
dp[i][0] &= 3dp[i – 1][0] + dp[i – 1][1] \\
dp[i][1] &= dp[i – 1][0] + 2dp[i-1][1] + dp[i – 1][2]\\
dp[i][2] &= dp[i – 1][1] + 2dp[i-1][2] + dp[i-1][3]\\
dp[i][3] &= dp[i – 1][2] + 3dp[i-1][3] \\
\end {align}
\]

したがって、正しい横棒の配置パターンを表すビット列を予め計算しておくことで、動的計画法の更新を行うことができます。

コード

提出したコード

ビット列の生成

vector<vector<int>> v;  // 横棒のパターン
int bit[8] = {};

// 正しい横棒のパターンの配列を追加する
void addBit() {
  int l = W - 1;
  for (int i = 1; i < l; i++) {
    if (bit[i - 1] == 1 && bit[i] == 1) return;
  }
  vector<int> tmp(l);
  for (int i = 0; i < l; i++) {
    tmp[i] = bit[i];
  }
  v.push_back(tmp);
}

// ビット列のパターンを再帰的に求める
void makeBit(int k) {
  if (k == W - 1) {
    addBit();
    return;
  }
  makeBit(k + 1);
  bit[k] = 1;
  makeBit(k + 1);
  bit[k] = 0;
}

動的計画法

  int l = v.size();
  for (int i = 1; i <= H; i++) {
    for (int j = 0; j < l; j++) {
      long* c = new long[W]();
      for (int k = 0; k < W; k++) {
        c[k] = dp[i - 1][k];
      }
      // swap() はビット列を見て値を交換するした値を c にコピーする。
      swap(dp[i - 1], v[j], c);
      for (int k = 0; k < W; k++) {
        dp[i][k] += c[k];
        dp[i][k] %= mod;
      }
    }
  }