[AtCoder] ABC 144 D – Water Bottle
問題
https://atcoder.jp/contests/abc144/tasks/abc144_d方針
水筒を傾けた時に入る水の最大値を考えます。傾けた時の角度を \( \theta \) とします。このときの水筒の容量を \( V (\theta)\) とします。そして、\( V (\theta) = x \) を満たす \( \theta \) を求めます。
\( 0 \leq \theta \leq \dfrac{\pi}{4} \) のとき
このとき、上部の線まで水を入れることができます。上部の三角形の面積を \( s \) とすると、
\[s = \dfrac{a^2 \tan{\theta}}{2}\]
となります。このとき、上部の体積は、\( as \) となるので、容量は、
\[ V( \theta) = a^2b – \dfrac{a^3 \tan{\theta}}{2}\]
となります。よって次のように方程式を解きます。
\[\begin{eqnarray}
a^2b – \dfrac{a^3 \tan{\theta}}{2} &=& x\\
\tan{\theta} &=& \dfrac{2(a^2b – x)}{a^3} \\
\theta &=& \tan^{-1} {\dfrac{2(a^2b – x)}{a^3}}
\end{eqnarray}\]
\( \dfrac{\pi}{4} \leq \theta \leq \dfrac{\pi}{2} \) のとき
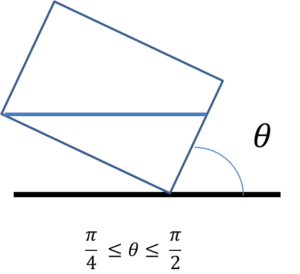
このとき、水筒の容量は下部の三角形の領域で表される体積となるので、下部の三角形の面積を \( s \) とすると、
\[s = \dfrac{b^2}{2\tan{\theta}}\]
となるので、容量は、
\[ V( \theta) = \dfrac{ab^2}{2\tan{\theta}}\]
となり、\( \theta \) は、
\[\begin{eqnarray}
\dfrac{ab^2}{2\tan{\theta}} &=& x\\
\tan{\theta} &=& \dfrac{ab^2}{2x} \\
\theta &=& \tan^{-1} { \dfrac{ab^2}{2x}}
\end{eqnarray}\]
とります。
また答えは、弧度法なので、
\[\dfrac{180\theta}{\pi}\]
とります。
コード
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const double PI=3.14159265358979323846;
int main() {
double a, b, x;
cin >> a >> b >> x;
double v = a * a * b;
double s;
if (2 * x < v) {
s = a * b * b / (2 * x);
} else {
s = (2 * (v - x) / (a * a * a));
}
double t = atan(s) * 180.0 / PI;
printf("%.10f\n", t);
return 0;
}